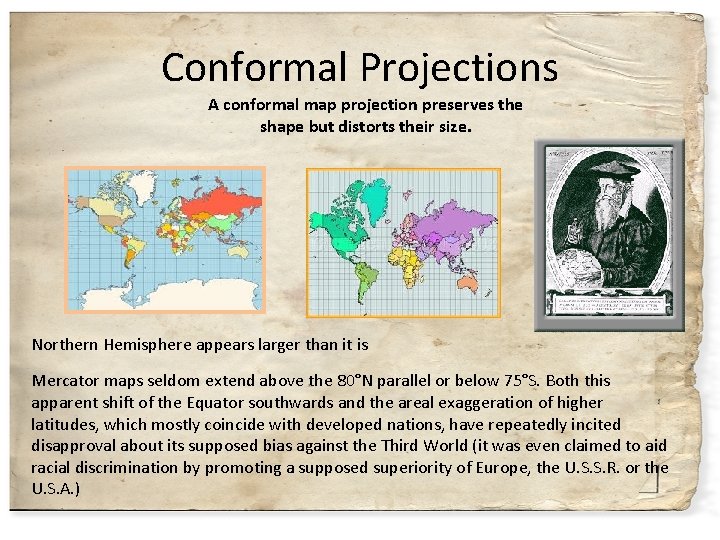
A Conformal Map Projection Is One That
A Conformal Map Projection Is One That
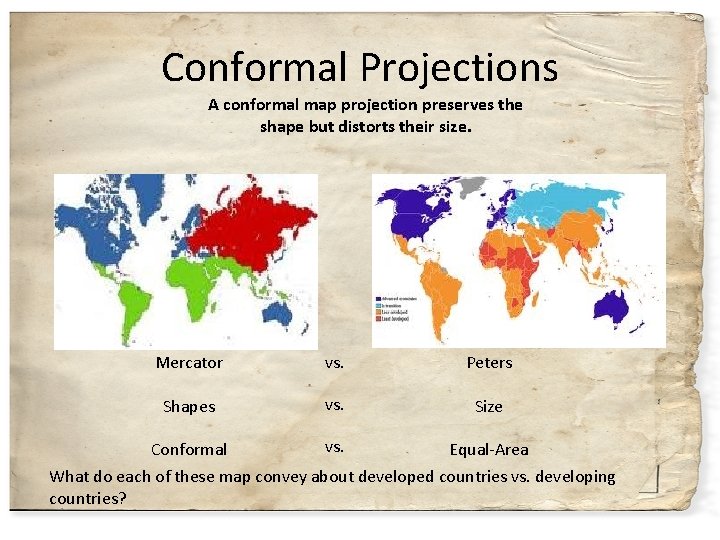
A Conformal Map Projection Is One That - Equal-area means that a spatial unit on one part of the map covers exactly an equal area of the actual Earth as a spatial unit of the same size in any other part of the map. Conformal map projections are the class of projections in which angles on the surface to be mapped are preserved tnat is corr. In other words an angle measured by a land surveyor anywhere on the Earths surface can be plotted at its corresponding location on a conformal projection without distortion.
Projections like this are called conformal projections.
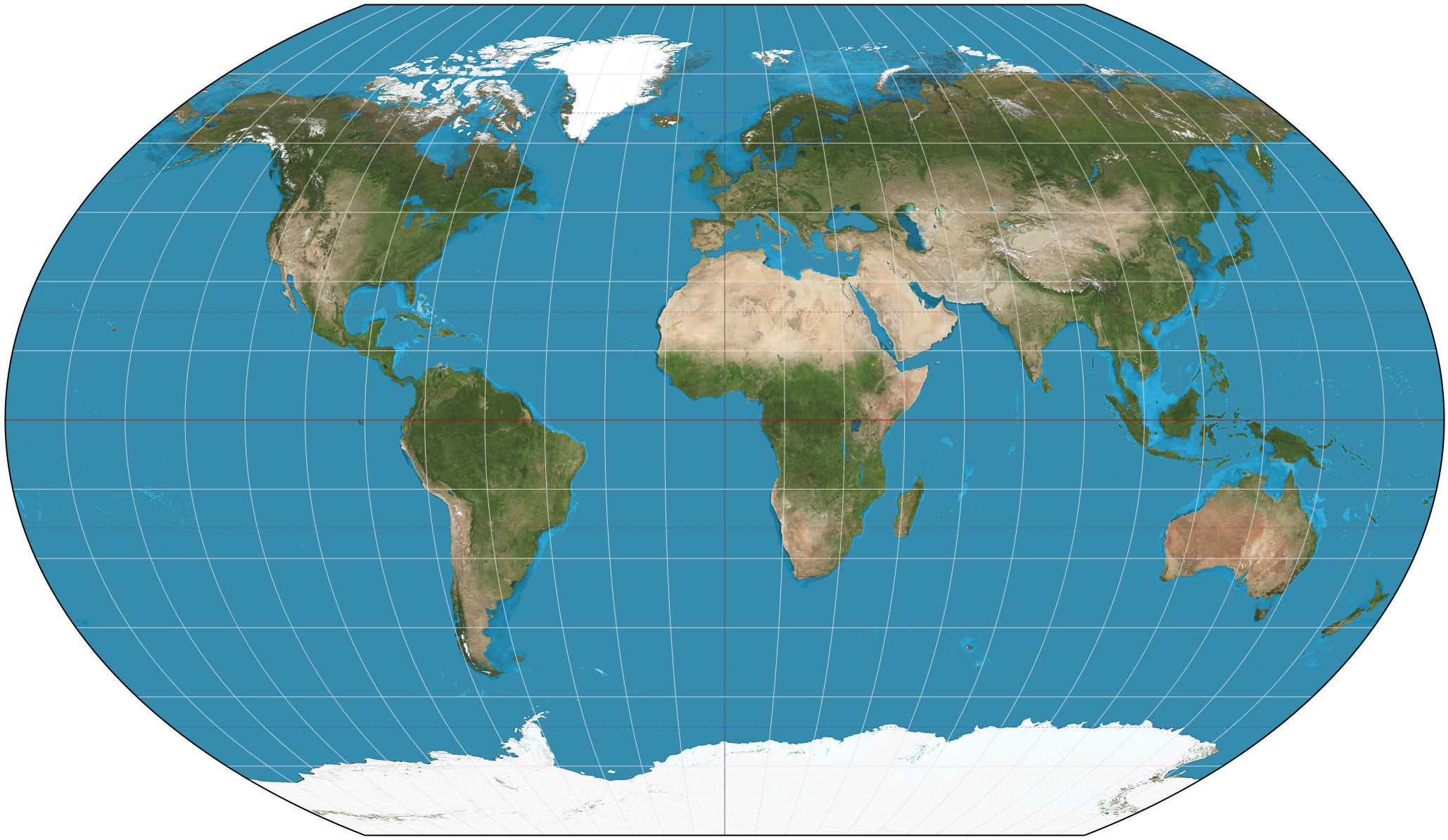
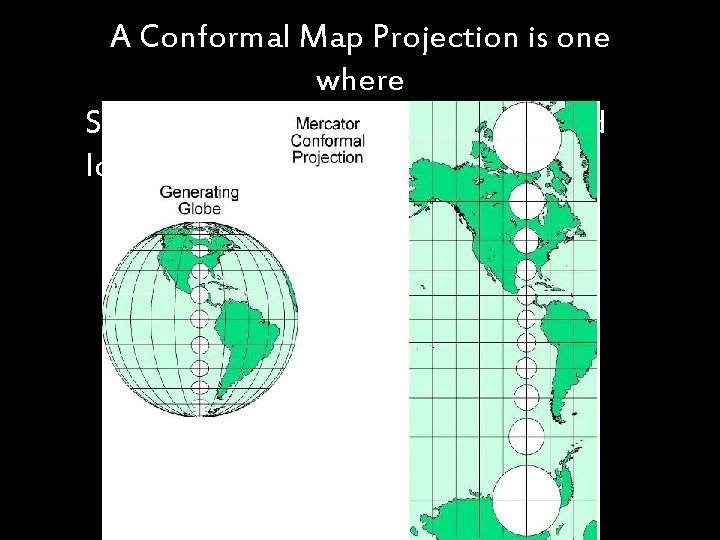
A Conformal Map Projection Is One That. In cartography a conformal map projection is one in which every angle between two curves that cross each other on Earth a sphere or an ellipsoid is preserved in the image of the projection ie. Tissots Indicatrices on the Mercator projection. Contrast that with a Lambert Conformal Conic below on the other hand which preserves the general form of the landmasses.
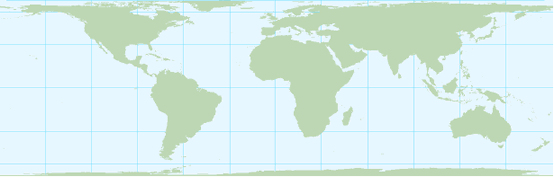
Examples are the Mercator projections the stereographic projections the conformal conical projections etc. This means that angles with short sides and shapes of small areas are shown correctly on the map. Comformal projections actually preserve local angles.
Under the hood this property is actually a little more complex. Conformal projections preserve the relative local angles about every point on the map so that meridians intersect parallels at 90 degrees. For a given point using the scale factor h along the meridian the scale factor k along the parallel and the angle θ between them.
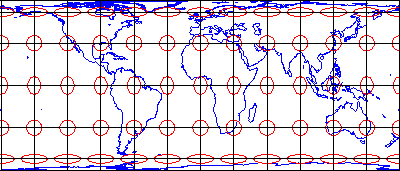
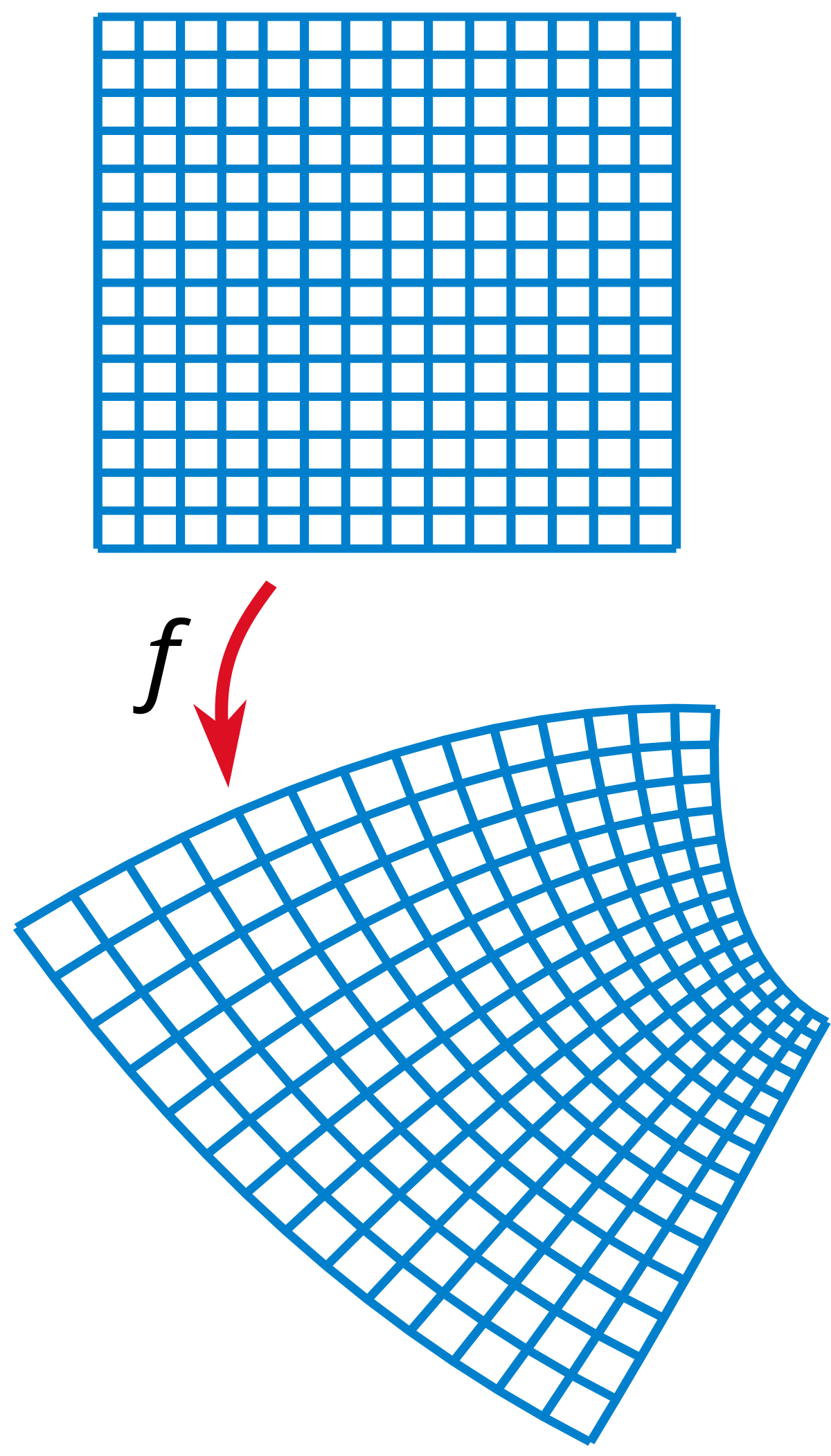
Indeed we see that near the origin fis nearly the identity only scaling by 4. Since any map projection is a representation of one of those surfaces on a plane all map projections distort. To preserve individual angles describing the spatial relationships a Conformal projection must show the perpendicular graticule lines intersecting at 90-degree angles on the map.
It is best suited for conformal mapping of land masses extending in an east-to-west orientation at mid-latitudes. We will restrict the surface to be mapped to be the ellipsoid as defined in geodesy. Note that the function lambdaxyis the stretching factor.
The projection is a conformal map in the mathematical sense. No map can be both equal-area and conformal. In a conformal orthomorphic map projection the angles between lines in the map are indentical to the angles between the original lines on the curved reference surface.
Parameters that define the Lambert Conformal Conic projection are the central meridian a reference latitude and two standard parallels. Near the origin thinking about the projection itself we expect little to no stretching. In particular letting lambdaxyfrac4x2y212 we see that fis a conformal map.
The consistent shapes indicate that conformal projections preserve the fidelity of angle measurements from the globe to the plane. This projection is conformal. Esponding angles on the map plane and the surface are equal.
In the sense that lines of latitude and longitude which are perpendicular to one another on the earths surface are also perpendicular to one another in the projected domain. Conformal projections Conformal projections preserve local shape. A map projection accomplishes this by maintaining all angles.
79 rows In standard presentation azimuthal projections map meridians as straight lines and. 04062020 Under conformal or orthomorphic map projections the scale depends only on the position of the point and not on the direction. Description The Lambert conformal conic map projection is typically based on two standard parallels but it can also be defined with a single standard parallel and a scale factor.
The classical way of showing the distortion inherent in a projection is to use Tissots indicatrix. The ellipses of distortion are circles.
1
Lab E Map Projections In Arcgis Eric Ching S Blog
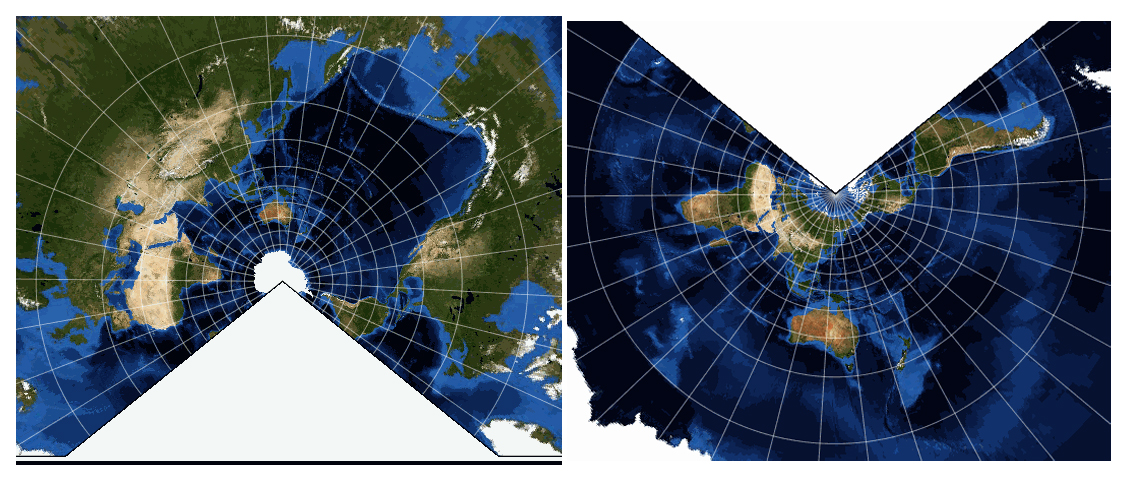Commonly Used Map Projections Intergovernmental Committee On Surveying And Mapping
Map Projections
Lab5 Map Projections Sergeevaanja S Blog
Unit 3 8 Deformation And Distribution Introduction To Geospatial Technology Using Qgis
Unit 3 7 Map Projection Properties Introduction To Geospatial Technology Using Qgis
Map Projection Wikipedia
Unit 3 7 Map Projection Properties Introduction To Geospatial Technology Using Qgis
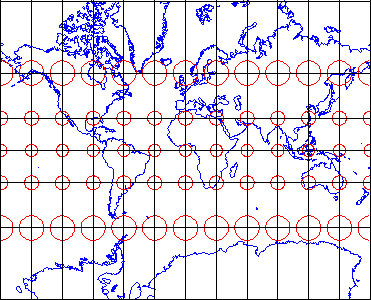28 Geometric Properties Preserved And Distorted The Nature Of Geographic Information
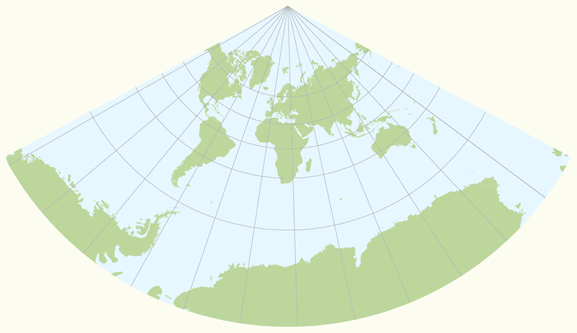Geometric Aspects Of Mapping Map Projections
Conformal Mapping From Wolfram Mathworld
Map Projections And How They Are Made Cartography
Map Projections
Charts And Projections Part Two
5gaqgh8a2lfo0m
Map Projections And How They Are Made Ppt Video Online Download
Unit 3 7 Map Projection Properties Introduction To Geospatial Technology Using Qgis
Conformal Geog 862 Gps And Gnss For Geospatial Professionals
Mercator Projection Wikipedia
Megan Wall Map Projections
Distortion Preservation On Conformal Mapping
Map Projection Wikipedia
Map Projections And How They Are Made Cartography
Map Projection Wikipedia
28 Geometric Properties Preserved And Distorted The Nature Of Geographic Information
8 Map Projected Using A Conformal Projection The Mercator Conformal Download Scientific Diagram
Geometric Aspects Of Mapping Map Projections
Week 6 Lab 1c Brynn S Blog
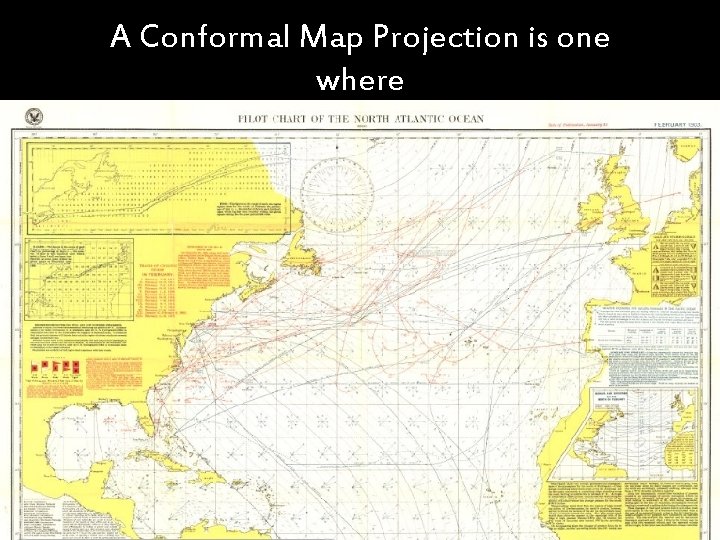Map Projection Theory And Usage What Is A
Conformal Map Wikipedia
F7qxwv4qlitrtm
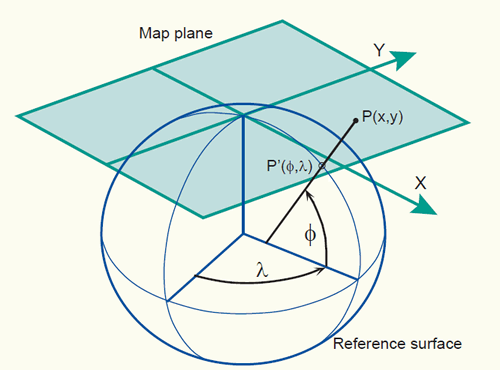Geometric Aspects Of Mapping Map Projections
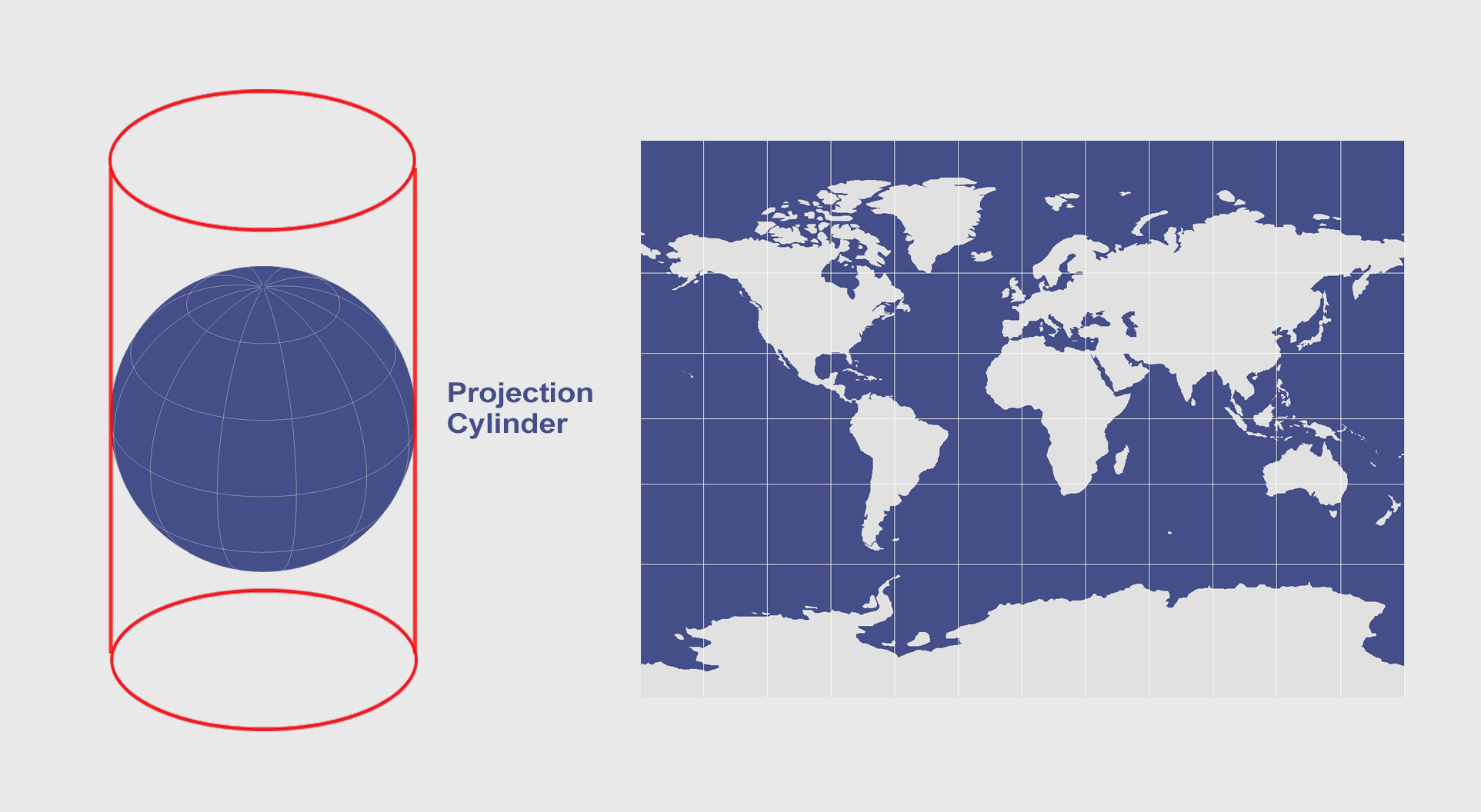Cylindrical Projection Mercator Transverse Mercator And Miller Gis Geography
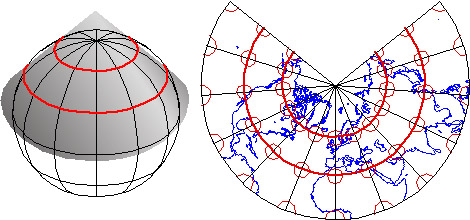2 3 What Are Map Projections Geog 160 Mapping Our Changing World
Types Of Map Projections Geography Realm
The Mercator Conformal Map Download Scientific Diagram
Conformal Map Projection Wikipedia
a.gif)
Geometric Aspects Of Mapping Map Projections
Post a Comment for "A Conformal Map Projection Is One That"